LES INSTRUMENTS DE PERCUSSION

Antoine Chaigne

1      Généralités sur les instruments de percussion.. 1

1.1       Classification sommaire. 1

1.2       Tour d’horizon sur les principes qui gouvernent la physique de ces instruments. 3

2      Présentation succincte du xylophone.. 5

3      Vibrations de flexion d’une lame de xylophone.. 7

3.1       Description et modèle. 8

3.2       Calcul des fréquences et des déformées propres de la lame. 10

3.3       Elaboration d’un clavier complet. 13

4      Interaction lame-excitateur.. 14

4.1       Maillets élastiques. Loi de Hertz. 14

5      Champ acoustique rayonné par un xylophone.. 18

6      Présentation succincte de la timbale.. 22

7      Interaction membrane-air dans les timbales. 25

8      Conclusion.. 27

9      Exemples sonores. 29

10    Bibliographie. 30

Le musicien distingue habituellement trois grandes classes d’instruments de percussion : les instruments de percussion à clavier, les peaux et les métallophones. Le premier point commun à ces trois classes est d’être mis en vibration par le biais d’un excitateur : baguettes de xylophone, mailloches de timbale, etc. Les propres mains du musicien peuvent même jouer ce rôle dans certains cas. Le second point commun réside dans le fait que ce sont les vibrations des structures ainsi excitées qui sont à l’origine du son émis.

Les instruments de percussion à clavier comportent des instruments en bois, en fibres de verre ou de carbone, tels que le xylophone ou le marimba. On y trouve également des instruments métalliques, comme le vibraphone, le glockenspiel ou encore les cloches d’orchestre tubulaires.

Figure 1 : xylophone.

Les peaux comportent : les tambours, les timbales, les caisses claires, les tablas indiens, les djembé,…et une multitude d’autres instruments propres à chaque culture.

Parmi les « métaux », on pourra citer les cymbales, le gong ou tam-tam chinois, les cloches, le triangle et les steeldrums.

Pour développer les principales idées de ce cours, nous adopterons le point de vue du physicien, sans perdre de vue, bien évidemment, qu’un instrument est fait avant tout pour être joué et écouté.

La quasi-totalité des instruments de percussion sont caractérisés par une phase d'interaction très courte avec un excitateur suivie d'un régime d'oscillations libres (voir lexique). On peut faire une distinction entre les instruments dont les vibrations libres sont linéaires (xylophone, timbale, cloches d'orchestre,...) dans la mesure où le choc initial de l'excitateur reste “suffisamment'' faible) et les instruments à vibrations non-linéaires (cymbales, gongs,...). Seuls les régimes de vibration linéaires seront traités dans ce cours.

En revanche, le comportement de l'excitateur lors de l'impact est, la plupart du temps, gouverné par une loi de déformation non-linéaire. Celle-ci détermine la forme et la durée de l'impulsion d'impact. Les impacts des excitateurs sont effectués sur des structures élastiques rigides (barres, plaques, coques) ou précontraintes (peaux de tambour, membrane de timbales). Dans ce cours, on abordera tout d'abord un exemple de structure élastique élancée que l'on peut raisonnablement étudier à l'aide d'un modèle de vibration monodimensionnel : la lame de xylophone. On étudiera ensuite un exemple de structure élastique précontrainte à deux dimensions : la membrane de timbale.

Dans bon nombre d'instruments de percussion, le champ acoustique émis par la structure vibrante est modifié par la présence, au voisinage de cette structure, de systèmes acoustiques passifs. Nous étudierons ici les effets de tubes résonateurs (cas des instruments de percussion à clavier) et de cavités (tambours, timbales, wood-blocks,...).

Lorsque le son est produit par des structures légères et souples, on ne peut plus négliger l'action exercée sur elles par la pression acoustique engendrée. On doit alors résoudre un problème d'interaction fluide-structure pour interpréter le fonctionnement de l'instrument. Cette propriété sera illustrée à nouveau par le cas de la timbale.

Le spectre d'amplitude des sons émis par les instruments de percussion est formé essentiellement de raies spectrales (ou partiels) de fréquences non harmoniques. En conséquence, la hauteur des sons produits est moins bien définie que pour d'autres familles d'instruments (piano, violon,...). On peut parfois rendre harmonique (ou quasi-hamonique) la série des partiels en modifiant la structure : c'est le cas des lames de xylophone que l'on creuse sur leur face arrière.

Le matériau joue un rôle essentiel dans les instruments de percussion, en particulier parce qu'il conditionne la durée du son émis et, par conséquent, le timbre de l'instrument.

Le xylophone est un instrument de percussion composé de barres (ou lames) libres mises en vibration par l’impact d’une baguette. Les barres sont faites généralement en bois, mais on trouve également des instruments faits en fibre de verre ou en fibre de carbone. Les lames sont percées sur le côté de manière à permettre le passage d’une cordelette souple qui les maintient en place.

Figure 2 : Fixation des lames de xylophone sur le clavier.

La section transversale des barres des instruments de percussion à clavier n’est pas uniforme (voir Figure 3). Cette variation de section est nécessaire pour accorder la barre (voir paragraphe 3).

Figure 3 : Vue de profil d’une lame de marimba. On aperçoit les deux trous qui sont destinés à laisser passer la cordelette de fixation. Le profil de section est ici déterminé pour que les trois premières fréquences propres de lame soient dans un rapport 1 :4 :10 (f₂ = 4 f₁ et f₃ = 10 f₁).

Dans certains modes de jeu de l’instrument, un résonateur tubulaire est placé sous chaque barre vibrante afin de modifier le champ acoustique rayonné par l’instrument (voir paragraphe 5). Dans ce cas, la longueur du tube est généralement ajustée de telle sorte que sa fréquence fondamentale soit proche de celle du premier partiel de la lame. La présence du résonateur modifie de manière significative l’évolution temporelle du son émis par la lame en ajoutant une « traînée sonore » quasiment monochromatique. Dans le domaine fréquentiel, on peut dire que l’action du résonateur se résume à une amplification et à un filtrage.

Figure 4 : Comparaison des formes d’onde de pression pour la note Sol₃ (G₄ selon la convention US) d’un xylophone. A gauche : sans résonateur ; a droite : avec résonateur.

Lorsqu’une barre libre est soumise à un impact, plusieurs types d’ondes sont susceptibles de s’y propager. Il s’agit principalement d’ondes de flexion verticale et horizontale, d’ondes de torsion et d’ondes longitudinales (voir Figures 5 et 6). Pour les excitations usuelles de l’instrument, on peut considérer que les régimes de vibrations de la lame restent linéaires : dans ce cas, toutes les ondes mentionnées ci-dessus sont découplées.

Figure 5 : Modes de vibration d’une lame de marimba (I) . A gauche : flexion verticale. A droite : torsion.

Figure 6 : Modes de vibration d’une lame de marimba (II) . A gauche : flexion horizontale. A droite : torsion.

Le son produit par l’instrument est essentiellement dû aux ondes de flexion verticale, c’est la raison pour laquelle nous ne nous intéresserons plus dorénavant qu’à celles-ci.

Figure 7 : Schéma du xylophone.

On montre, en théorie de l’élasticité, que les vibrations de flexion d’une lame homogène et isotrope de section variable S(x), de densité r, de module d’Young E, de longueur L, de largeur b << L, de hauteur h(x) et de masse M_B (voir Figure 7) sont gouvernées par le système d’équations suivant :

                                                     (1)

            (2)

Où M(x,t) est le moment de flexion en un point courant d’abscisse x de la barre à l’instant t, I(x) est le moment d’inertie de la lame par rapport à la fibre neutre selon l’axe x, h est un coefficient d’amortissement viscoélastique du matériau, g_B est un coefficient d’amortissement de type fluide, w(x,t) est le déplacement transversal de la lame et c est une constante de rappel qui représente l’action de la cordelette. Le terme f(x,xo,t) représente l’action de la baguette (voir paragraphe 4).

La section S(x) et le moment d’inertie I(x) sont reliés aux autres variables géométriques par les formules :

                                                     (3)

Enfin, les conditions aux limites libres aux bords de la lame se traduisent par les expressions

                                                                   (4)

qui expriment que les forces et les moments exercés aux extrémités de la lame sont nuls.

L’ensemble des équations (1) à (4) constitue ce que l’on appelle classiquement le modèle d’Euler-Bernoulli unidimensionnel pour une barre isotrope (voir Graff). On a montré que ce modèle rend bien compte du fonctionnement de la plupart des instruments de percussion à clavier (xylophone, marimba, vibraphone, glockenspiel,…) dans leur registre grave. Par contre, il s’avère insuffisant pour interpréter convenablement le fonctionnement de ces instruments dans l’aigu (voir Chaigne et Doutaut). Néanmoins, nous nous contenterons de ce modèle dans toute la suite de ce cours.

Figure 8 : Orthotropie du bois.

Dans le cas des barres en bois, on peut légitimement s’interroger sur la pertinence d’un modèle isotrope dans la mesure où le bois est un matériau orthotrope (voir figure 8). En réalité, si les lames sont taillées dans la direction des fibres (ce qui est pratiquement toujours le cas), il est possible de modéliser le matériau bois par un matériau isotrope équivalent. Ceci n’est possible que parce que la largeur b des lames est faible devant leur longueur. Dans le cas des plaques, (une table d’harmonie de guitare ou de piano, par exemple), il serait nécessaire de tenir compte de l’anisotropie du matériau.

Le système d’équations (1) à (4) est bien trop complexe pour que l’on puisse espérer obtenir une solution analytique au problème. Seule une approche numérique est envisageable.

Néanmoins, nous allons examiner ci-dessous une version simplifiée de ces équations qui offre l’avantage de bien faire comprendre le fonctionnement de l’instrument et, en particulier, la nécessité de creuser les lames pour les accorder. Dans ce paragraphe, nous allons donc étudier les vibrations libres non amorties d’une barre de section constante, pour laquelle il existe une solution analytique. De cette étude, nous allons déduire les expressions des fréquences propres et déformées propres de la lame.

Pour simplifier le problème, nous sommes dans l’obligation de faire plusieurs hypothèses qui vont nous permettre au passage de préciser le rôle des différents termes dans les équations (1) et (2) ci-dessus :

1.      On néglige, pour l’instant, le terme source f(x,x_o,t) qui représente l’action de la baguette.

2.      On ne tient pas compte du terme c dont le rôle est simplement d’assurer une force de rappel afin d’éviter que la lame n’effectue un mouvement de corps rigide jusqu’à l’infini (rôle de la cordelette).

3.      On laisse de côté provisoirement les termes d’amortissement qui, s’ils sont essentiels pour rendre compte du rôle du matériau dans la qualité sonore de l’instrument, ne perturbent que faiblement les fréquences et les déformées propres.

Enfin, nous allons provisoirement considérer pour commencer le cas où S(x) = So = cte.

Une fois connue la solution analytique, nous pourrons revisiter chacune de ces hypothèses simplificatrices afin d’examiner qualitativement leur influence.

Compte tenu de ces simplifications, les équations (1)-(2) se réécrivent :

                                                                                     (5)

Pour calculer les fréquences propres de la barre qui forment le contenu spectral des oscillations libres, on procède en recherchant des solutions de la forme :

                                                                                      (6)

Dans ce cas, l'équation (5) devient :

                                                                                   (7)

La résolution de l’équation (7) fournit alors la solution générale :

                 (8)

avec

                                                                                        (9)

On remarque en particulier que v, qui s'identifie avec la célérité de propagation des ondes de flexion dans la barre, dépend de la pulsation w. Ceci signifie que l'on a affaire à des ondes dispersives. La célérité de propagation augmente avec la fréquence. En conséquence une impulsion de flexion va se déformer au cours du temps.

Remarque : L’équation (9) fait apparaître un phénomène paradoxal, à savoir que la vitesse de phase des ondes élastiques de flexion dans la barre tendrait vers l’infini avec la fréquence. Il n’en est rien évidemment. Ce paradoxe apparent est dû au modèle simplifié d’Euler-Bernoulli qui néglige les effets de rotation inertielle de la barre et la déformation des sections droites due au cisaillement. Lorsque l’on introduit ces deux phénomènes dans le modèle de barre (modèle de Timoshenko), on trouve alors que la célérité des ondes de flexion varie en  en basses fréquences puis tend vers une asymptote lorsque la fréquence augmente, ce qui est plus raisonnable.

Pour poursuivre le calcul, on introduit les conditions aux limites libres, ce qui donne :

                                                                           (10)

                                                                           (11)

                                                                            (12)

On aboutit finalement à l'équation des fréquences propres pour une lame de section constante libre aux deux extrémités (voir Figure 9) :

                                                                            (13)

Figure 9 : Résolution graphique de l’équation (13), avec .

Une résolution numérique de (13) montre alors que les fréquences propres correspondantes f_n (en Hz) sont données par :

                                                (14)

On remarque que, contrairement au cas d’une corde idéale, les fréquences propres de flexion de la barre de section constante sont inharmoniques, c'est-à-dire qu'elles ne sont pas multiples entières d'un fondamental. Cette propriété est visible sur la Figure 10 qui montre le spectre d'amplitude de vibration d'une lame de section constante. Sur cette même figure, on peut voir un pic spectral supplémentaire voisin de zéro (qq. Hertz) qui correspond à la résonance de suspension des lames. Cette résonance, non prévue par l'équation (13) ne produit aucun son.

Figure 10 : Spectre d'amplitude vibratoire d'une barre de section constante.

Du point de vue de la perception de hauteur, l'inconvénient majeur d'un spectre inharmonique est que la (ou les) hauteur(s) perçues sont moins nettes que pour un spectre harmonique. Pour cette raison, les facteurs d'instruments de percussion à clavier taillent les lames sur leur partie inférieure. Lorsque la lame est ainsi taillée, le problème aux fréquences propres s'exprime en remplaçant  par  et S_o par S(x) dans les équations initiales de la lame (1)-(2).

Dans ce cas, comme nous l’avons dit plus haut, il n'existe pas de solutions analytiques à ces équations et l'on doit se contenter d'une approximation numérique. On montre qu'il est possible d'optimiser la largeur et la profondeur de la taille (tout en respectant d'autres critères comme, par exemple, la non-apparition de vibrations de torsion ou la limite d'élasticité de la lame) afin de faire en sorte que les partiels d'ordre supérieur à 1 soient des multiples entiers du fondamental. C'est le cas de la Figure 11 qui montre un exemple de spectre d'amplitude vibratoire de barre creusée pour laquelle on voit (outre la résonance de suspension) trois ``pics'' spectraux à 440, 1760 et 3960 Hz. On remarque donc que la taille est telle que  et . On retrouve donc bien le spectre d'un son périodique, même si certains harmoniques ,…sont absents.

Figure 11 :  Spectre d'amplitude vibratoire d'une barre de section variable.

Pour élaborer un clavier complet, on doit, outre les considérations précédentes, tenir compte de la jouabilité de l’instrument. ceci impose, entre autre, une largeur minimale pour les lames.

Les claviers d’instruments de concert font généralement 3 octaves ½ ou 4 octaves. Dans ce cas, cela signifie qu’il y a un rapport 16 de fréquences entre la note la plus aiguë et la note la plus grave de l’instrument. Or, l’équation (14) a montré que les fréquences variaient comme l’inverse du carré de la longueur des lames. Autrement dit, on pourrait s’attendre à ce qu’il y ait un rapport 4 entre les lames les plus longues et les lames les plus courtes. Dans la réalité, on constate que ce rapport ne dépasse jamais 3. La raison principale provient de ce que l’accord des lames est d’autant plus difficile que les lames sont courtes, car alors, comme nous l’avons mentionné plus haut, le modèle unidimensionnel d’Euler-Bernoulli perd sa validité. En pratique, le facteur joue simultanément sur la longueur (pour un facteur 3) et sur la taille inférieure de la lame (pour un facteur 4/3) afin de répartir les notes tout le long du clavier.

Le modèle ci-dessus est d’autant plus exact que l’épaisseur des lames reste faible. Cependant, l’épaisseur ne peut descendre en pratique en dessous de 15 à 20 mm (pour un xylophone en bois) sous peine de fragiliser par trop les lames. En effet, l’intensité des chocs reçus par les lames peut s’avérer suffisamment forte pour entraîner leur rupture.

Outre le soin accordé à l’accord des lames, le choix des matériaux et l’homogénéité d’ensemble du clavier jouent un rôle primordial dans la qualité sonore de l’instrument. S’il s’agit de bois, les lames devront être sélectionnées une par une afin d’écarter celles qui présentent des nœuds, des fissures ou des inhomogénéités manifestes. Les matériaux tels que les fibres de carbone ou les fibres de verre offrent l’avantage de présenter des caractéristiques élastiques plus homogènes et plus reproductibles que le bois. Par contre, les ondes de flexion s’amortissent plus lentement dans ces derniers matériaux que dans les bois usuels pour ces instruments que sont le bois de Padouk ou le palissandre. En conséquence, le timbre en est significativement différent. La plupart des musiciens préfèrent généralement le timbre du palissandre.

Lorsque la tête d’une baguette, supposée parfaitement élastique, rentre en contact avec une lame de xylophone, la force d’interaction F(t) entre les deux solides en contact est régie en première approximation par la loi de Hertz (voir Landau), à condition que la déformation des deux solides en contact reste faible. Cette loi stipule que l’expression de la force est donnée par :

                                                                           (15)

Où la constante de raideur K dépend de la géométrie ainsi que des propriétés élastiques des deux surfaces en contact. La variable z(t) représente le déplacement du centre de gravité de la tête et w(x_o,t) représente le déplacement de la barre au point d’impact.

L’équation (15) perd de sa validité en grande déformation (cas d’un fort impact avec une tête en caoutchouc, par exemple) ou lorsque la lame subit des modifications plastiques sous l’effet du choc.

Remarque : pour les mailloches de timbale (et les feutres de marteau de piano) plusieurs auteurs ont proposés des modèles empiriques qui se rapprochent formellement de l’équation (15), à la différence près que l’exposant r est réel ( 2<r<3, généralement) et non plus égal à 3/2.

Figure 12 : Exemples de mailloches de timbale.

Figure 13 : Compression d’une tête de mailloche pour obtenir sa caractéristique force/déformation.

Figure 14 : Caractéristiques expérimentales force-déformation de mailloches de timbales.

Pour compléter le modèle d’excitation du xylophone, on écrit le principe fondamental de la dynamique appliqué au centre de gravité du maillet, ainsi que les conditions initiales :

                                                       (16)

Où V₀ est la vitesse verticale de la tête de la baguette au moment de l’impact. Il est possible de raffiner ce modèle en tenant compte de la flexibilité du manche de la baguette.

Les équations de fonctionnement de la lame (Equations 1 et 2) sont des équations locales. Pour insérer le terme d’excitation, il est donc nécessaire de définir non pas une force mais une « densité de force », afin de respecter l’homogénéité des variables. On fait, tout d’abord, l’hypothèse légitime que les parties temporelles et spatiales de f(x,x_o,t) sont séparables. On écrit donc :

f(x,x_o,t) = f(t) g(x,x_o)                                                                                (17)

Où g(x,x_o) est une fenêtre qui régit la distribution spatiale de la force d’impact autour du point x_o, sur un intervalle de largeur 2 dx. Dès lors, la distribution temporelle de l’impact s’écrit, compte tenu de l’expression de la force d’impact F(t) définie plus haut :

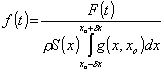                                                                         (18)

Le modèle d’impact décrit ci-dessus permet de prédire les caractéristiques essentielles de l’impulsion de force communiquée par l’instrumentiste à la lame, à savoir sa durée et son intensité. L’intensité de la force gouverne directement l’intensité du son produit, tandis que sa durée impose la largeur du spectre excité : l’impulsion de force engendrée par un maillet à tête souple sera plus large que pour un maillet à tête rigide. En conséquence, la largeur du spectre excité sera plus faible dans le premier cas que dans le second ce qui produira un son plus « mat » ou encore moins « brillant ». Pour varier la couleur sonore, les musiciens disposent en général d’un grand nombre de baguettes, comme on peut s’en rendre compte en jetant un coup d’œil du côté du pupitre des percussionnistes, lors d’un concert symphonique.

Le champ acoustique rayonné par un xylophone est composé de deux parties : le champ sonore « primaire » rayonné par la lame frappée et le champ sonore « secondaire » rayonné par le résonateur, dont la colonne d’air est excitée par le champ primaire issu de la lame.

Figure 15 : Schéma du champ rayonné par le xylophone. Définitions des variables.

On fait l’hypothèse (vérifié par l’expérience, voir Figure 16) que le champ secondaire rayonné par l’ouverture du tube résonateur n’influe pas sur le comportement vibratoire de la lame.

Figure 16 : Spectres de vibration d’une lame de xylophone (note Fa₃, ou F₄ en convention US). A gauche : sans résonateur. A droite : Avec résonateur. On constate qu’il n’y a aucune différence entre les deux spectres.

La géométrie de la lame (L >> b et L >> h) est telle que l’on peut calculer le rayonnement de celle-ci en la représentant par un réseau linéaire de petites sphères oscillantes (voir figure 17).

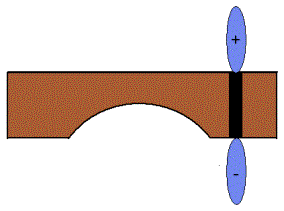
Figure 17 : Représentation du rayonnement de la lame seule par un réseau linéaire de sphères oscillantes.

Dans ce cas, on montre (Junger, Pierce) que la contribution en pression de chaque sphère élémentaire s’écrit :

          (19)

où Dp_i est la contribution de la sphère oscillante de volume élémentaire DV_i au point d’abscisse x_i sur la lame, mesurée en un point récepteur repéré par les coordonnées () dans l’espace (voir Figure 15). La quantité c_o est la célérité du son dans l’air et  la masse volumique de l’air. Si l’on suppose que la lame est découpée en N segments élémentaires, on obtient alors le champ total p_B rayonné par la lame en sommant sur l’ensemble du réseau :

                                                                               (20)

Du point de vue du rayonnement, une lame de xylophone se comporte donc comme une antenne dipolaire rectiligne. La propriété essentielle d’un tel réseau est sa directivité. On constate en effet (Tuttle) que les lames rayonnent beaucoup plus d’énergie dans l’axe vertical que dans le plan du clavier.

Pour le calcul du champ rayonné par le résonateur, on va faire le choix que le tube est fermé à son extrémité inférieure. Etant donné le registre de l’instrument, on se trouve la plupart du temps dans la situation où l’on peut raisonnablement admettre que seules des ondes planes se propagent dans le tube. Pour simplifier les écritures, on va négliger ici les pertes viscothermiques dans le tube. Signalons, toutefois, que ces pertes doivent être prises en compte si l’on veut obtenir des synthèses sonores réalistes à l’aide du modèle physique présenté ici.

On obtient donc dans le tube l’équation des ondes en pression :

                                                                             (21)

Et à l’extrémité fermée  (en l = l_T):

                                                                                              (22)

A l’extrémité ouverte, on écrit que le champ de pression total est la somme de la contribution de la lame en ce point et de la contribution propre du tube. Celle-ci est gouvernée par l’impédance de rayonnement du tube. On obtient donc (écrit, dans un premier temps dans le domaine fréquentiel ^*) :

                                                  (23)

Où S_T est l’aire de la section droite du tube cylindrique et u la vitesse acoustique à l’ouverture. Afin de retrouver une formulation en pression, on peut combiner cette dernière équation avec l’équation d’Euler, ce qui donne, en sortie du tube :

                            (24)

^*Remarque : on peut exprimer cette dernière équation dans le domaine temporel. Dans ce cas il est nécessaire d’utiliser une formulation approchée de l’impédance de rayonnement qui conserve la stabilité des équations. Il s’agit d’une question délicate qui déborde du cadre de ce cours (voir Doutaut et al.).

La dernière étape du calcul consiste à calculer le champ de pression secondaire rayonné en tout point de l’espace à partir de l’expression obtenue ci-dessus pour le champ à la sortie du tube. On néglige ici les effets d’obstacle dus à la présence des lames et des autres tubes résonateurs voisins. Ces hypothèses sont légitimes tant que les lames ne sont pas « trop près » du tube (quelques cms, en pratique, pour les longueurs d’onde usuelles) et tant que les tubes voisins ont une section « faible » (idem, quelques cms de diamètre). On peut alors admettre que le champ rayonné par l’extrémité ouverte du tube est monopolaire, ce qui veut dire qu’il correspond à celui d’une petite « sphère pulsante » à l’extrémité du tube. Dans ce cas, le diagramme de rayonnement du tube possède la symétrie sphérique, ce qui est vérifiable expérimentalement. Pour un tel monopole, la pression à une distance r_T de l’extrémité du tube s’écrit :

                                                          (25)

Au total, la pression rayonnée par un ensemble « lame+résonateur tubulaire » s’écrit :

                                                    (26)

il est intéressant de souligner que l’allure temporelle du signal de pression reçu dépend fortement de la position du récepteur (oreille humaine ou microphone) (voir figures XXX). Cette propriété est une conséquence directe de la directivité du diagramme de rayonnement de la lame seule, le rayonnement du tube étant, lui, omnidirectionnel.

Figure 18. Pression rayonnée par le xylophone. A gauche : dans l’axe vertical (q = 0°). A droite : quasiment dans le plan horizontal (q = 80°).

Pour la prise de son, il est donc important de savoir qu’en plaçant le microphone au-dessus du clavier (q = 0°), on privilégiera le son des lames, tandis qu’un microphone placé dans le plan du clavier (q = 90°) va privilégier, au contraire, la contribution des résonateurs. On passe graduellement de l’une à l’autre contribution en faisant varier l’angle q (voir Figure 18).

Le xylophone, présenté ci-dessus, illustrait le cas d’un instrument percussif où il est possible de calculer séparément le régime vibratoire et le rayonnement acoustique.

Il n’en est pas toujours ainsi, en particulier lorsque les surfaces vibrantes d’un instrument sont légères et souples. Dans ce cas, le champ de pression rayonné par la surface vient modifier son comportement vibratoire qui lui même influence le rayonnement. On a affaire à un « système bouclé » et il nécessaire de traiter globalement ce problème de vibroacoustique.

Nous allons illustrer ces phénomènes à propos de la timbale. Les timbales sont des instruments de percussion composés d’une fine membrane (ou peau) circulaire en Mylar tendue sur un fût qui renferme une cavité d’air. Le petit trou situé au fond de la cavité sert à égaliser les pressions statiques de part et d’autre de la membrane. Il joue ainsi le même rôle que la trompe d’Eustache dans l’oreille moyenne qui permet d’égaliser les pressions de part et d’autre du tympan.

Figure 19 : La famille Adams…

Les vibrations de la membrane sont couplées avec l’air extérieur et la cavité interne. En champ libre, l’air extérieur agit essentiellement par son inertie, si bien que son effet principal est de diminuer les fréquences propres de la membrane, par rapport au cas théorique in vacuo. Les effets de la cavité sont plus complexes : suivant les fréquences, et suivant l’endroit de l’excitation, on peut constater soit une diminution complémentaire, soit une augmentation des fréquences propres. Ces effets variables sont dus au fait que l’effet prépondérant de la cavité est, suivant la fréquence et la position de l’impact, tantôt un effet de raideur, tantôt un effet d’inertie.

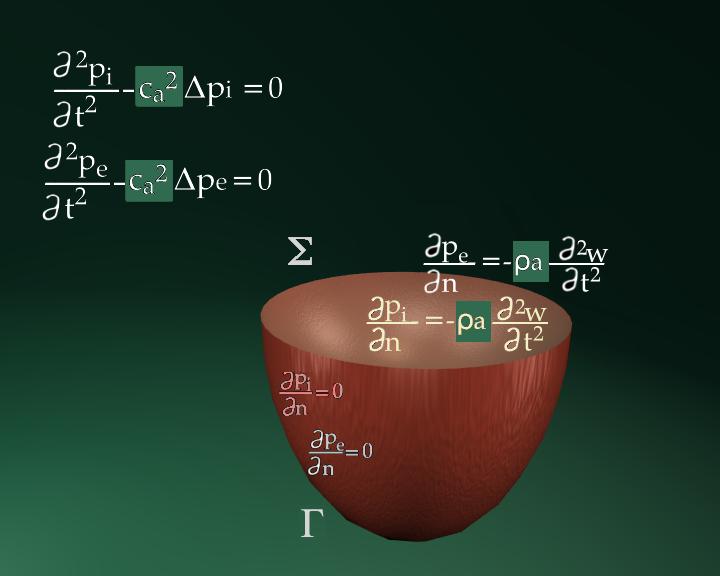
Figure 20 : Présentation des variables de base pour la membrane, les champs acoustiques et le fût de la timbale.

Figure 21 : Présentation des variables de base pour la mailloche en interaction avec la membrane.

Le modèle d’excitation pour la timbale peut être calqué à peu de choses près sur celui du xylophone. Par contre, l’équation de vibration de la membrane comprend, au second membre, un terme source supplémentaire qui correspond aux forces de pression interne et externe. Le terme h correspond aux pertes dans le matériau qui interviennent dans l’amortissement des vibrations de la membrane et, par conséquent dans le timbre du son. Ainsi, pour une membrane de timbale de densité massique s (en kg/m²) et de tension T (en N/m), l’équation des vibrations transversales s’écrit :

                                            (27)

Dans l’équation (27), la quantité  a la même signification que dans (2), et représente donc l’impulsion de force communiquée par l’impact de la mailloche. La nouveauté réside ici dans la présence du saut de pression  entre l’air externe et l’air interne, de part et d’autre de la membrane S. La membrane est, en outre, supposée fixée rigidement à sa périphérie , ce qui s’écrit :

                                                          (28)

Les champs acoustiques dans l’espace intérieur (W_i) et extérieur (W_e) sont, eux, régis par les équation des ondes complétées par les conditions aux limites sur la membrane S et sur le fût F (Figure 20) :

                                                (29)

L’équation qui exprime la continuité des vitesses normales à travers la membrane est donnée par :

                                (30)

Sur le fût F, l’hypothèse de rigidité parfaite revient à écrire :

                                         (31)

où n est le vecteur normal au fût. Pour que le problème soit complet il est nécessaire, enfin, de rajouter des conditions initiales pour la mailloche et la membrane.

Il est clair que le problème est, ici encore, bien trop complexe pour pouvoir être traité analytiquement. Nous allons présenter ci-dessous les résultats de simulations numériques, validées par l’expérience, qui illustrent l’évolution temporelle des variables vibratoires et acoustiques dans une timbale, à partir de l’instant où la mailloche frappe la peau (voir le site http://www.inria.fr/multimedia/CentreVirtuelDemos/timbale.html).

(Animation vidéo : Timbale_cube.mpg).

Les images ci-dessous (Figure 22) illustrent l’évolution du déplacement de la membrane au cours des 10 premières millisecondes du son. La membrane s’enfonce en (a) sous l’effet de la mailloche. En conséquence, un front d’onde se développe en amont de la position de l’impact en (b)-(c). En (d), le front d’onde (positif) commence à se réfléchir sur le bord avec changement de signe (e). Il en résulte à nouveau une onde retour (positive) qui vient repousser la mailloche.

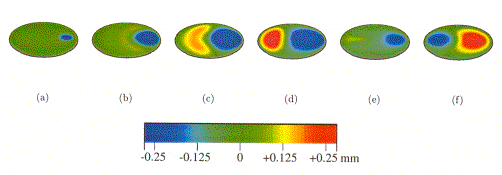
Figure 22 : Evolution du déplacement de la membrane pendant les dix premières millisecondes du son.

La figure suivante (Figure 23)  montre, à son tour, l’évolution temporelle des champs de pression interne et externe au cours du même laps de temps. En (a), l’impact engendre une surpression à l’intérieur de la cavité qui se propage à une vitesse plus rapide que l’onde élastique sur la membrane. Le champ interne est, bien entendu, contraint par la forme du fût. De (b) à (f), on constate que la directivité du rayonnement acoustique externe évolue de manière complexe au cours du temps.

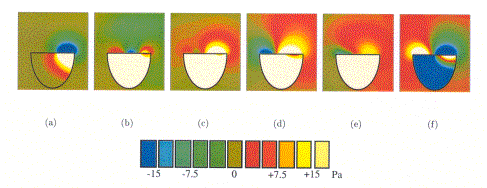
Figure 23 : Evolution des champs de pression interne et externe pendant les dix premières millisecondes du son.

Lorsque la tension de la membrane n’est pas uniformément répartie (Figure 24), on constate des battements à l’écoute. L’origine de ces battements, dus à des inhomogénéités de contraintes au sein de la membrane, est confirmée par l’analyse spectrale qui fait apparaître des fluctuations d’intensité des principaux partiels du son au cours du temps (Figure 25).

Figure 24 : Répartition inhomogène de la tension au sein de la membrane. La tension varie entre 3100 N/m (en blanc) et 3317 N/m (en noir). Cette répartition correspond au cas d’une membrane tendue par six vis de serrage à sa périphérie, deux d’entre elles étant moins serrées que les autres.

Figure 25 : Spectrogramme 3D (Intensité-temps-fréquence) d’un son de timbale dont la peau est légèrement désaccordée.

      Au long de ces quelques pages, nous n’avons pu donner qu’un aperçu de la physique des instruments de percussion à clavier et à membranes. Nous espérons avons pu montrer au lecteur que le fonctionnement de ces instruments est parfois plus complexe que cela peut paraître au premier abord. Dans la bibliographie ci-dessous, on pourra constater que plusieurs articles majeurs sur le sujet datent de moins de dix ans, ce qui témoigne d’une vitalité certaine de la recherche en ce domaine. Cela indique également que la modélisation physique précise de ces instruments n’est établie que depuis une période relativement récente, bien que les principes généraux en soient connus depuis le début du XXème siècle environ. Les progrès en matière de simulation numérique et d’expérimentation ont été à la base de ces progrès récents.

      La famille des métaux (cymbales, gongs,…) reste aujourd’hui la plus mal connue. Il n’existe à l’heure actuelle aucun modèle physique capable de reproduire de façon convaincante les sons générés par ces instruments. La difficulté majeure rencontrée ici provient du fait que les amplitudes de vibrations sont comparables, voire supérieures, à l’épaisseur des solides en vibrations. Par conséquent, nous sommes confrontés à des régimes fortement non-linéaires pour lesquels même les méthodes mathématiques connues (méthodes d’échelles multiples, …) s’avèrent la plupart du temps insuffisantes. Il s’agit donc d’une problématique de recherche importante, qui dépasse même le cadre strict de l’acoustique musicale. Il faudra vraisemblablement attendre encore quelques années avant de pouvoir disposer d’un modèle fiable et cohérent pour ces instruments.

1.      Comparaison de l’effet d’un tube résonateur sur le son d’une lame de xylophone

(Séquence : Sans résonateur ; avec résonateur ; sans résonateur ; avec résonateur).

2. Comparaison entre mesure et simulation d’un son de vibraphone.

(Séquence : mesure ; simulation ; mesure ; simulation).

3. Synthèse sonore d’un fragment de Peer Gynt (lame de xylophone seule).

4. Synthèse sonore d’un fragment d’une Sonate pour violon seul de Bach (lame + résonateur).

5. Synthèse sonore d’une séquence de vibraphone.

1. T. D. Rossing, ``Acoustics of percussion instruments: Part II'', Phys. Teach. 15, 278-288 (1977).

2. A. Chaigne & V. Doutaut, ``Numerical simulations of xylophones. I. Time-domain modeling of the vibrating bars'', J. Acoust Soc. Am. 101(1), 539-557, (1997).

3. V. Doutaut, D. Matignon & A. Chaigne, ``Numerical simulations of xylophones. II. Time-domain modeling of the resonator and of the radiated sound pressure'', J. Acoust Soc. Am. 104(3), 1633-1647, (1998).

4. L. Rhaouti, A. Chaigne & P. Joly, ``Time-domain modeling and numerical simulation of a kettledrum'', J. Acoust. Soc. Am. 105(6), 3545-3562, (1999).

5. F. Orduña-Bustamente, ``Nonuniform beams with harmonically related overtones for use in percussion instruments'', J. Acoust. Soc. Am. 90, 2935-2941, (1991).

6. K. F. Graff, Wave motion in elastic solids, Dover, New York, (1991).

7. L. Landau & E. Lifchitz, Théorie de l’élasticité, Editions Mir, Paris, (1967).

8. I. Bork, ``Measuring the properties of mallets'', Appl. Acoust. 30, 207-218, (1990).

9. I. Bork, ``Practical tuning of xylophone bars and resonators'', App. Acoust. 46, 103-127, (1995).

10. V. Bucur, Acoustics of wood, Editions CRC, Boca Raton, (1995).

11. M. C. Junger, ``Sound radiation by resonances of free-free beams'', J. Acoust. Soc. Am. 52, 332-334, (1972).

12. A. D. Pierce, ``Acoustics. An introduction to its physical principles and applications'', Acoustical Society of America, New York, (1989).

13. B. C. Tuttle & C. B. Burroughs, ``The effects of a resonator tube on the timbre and directivity of sound radiation from a vibraphone bar'', in Proceedings of the Institute of Acoustics – ISMA’97, Vol. 19(5), 207-211, (1997).

14. T. D. Rossing, ``The physics of kettledrums'', Sci. Am. 247, 172-178, (1982).

15. R. E. Davis, ``Mathematical modeling of the orchestral timpani'', Ph. D. thesis, Physics Department, Purdue University, (1988).